We have introduced a two-parameter turbulence algorithm (Ivanova and others 2022) into the RAMMS powder avalanche model (Bartelt and others, 2016). Use of the turbulence model provides slightly higher estimates of powder cloud impact pressures, especially at locations that are near to the avalanche core. The turbulence model also predicts larger lateral spreading, and thus larger cloud inundation areas. We use vortex turnover times to estimate loading duration times on structures (Caviezel and others, 2021) and to predict dynamic magnification factors for tree blow down (Bartelt and others, 2018).
To understand how the model works let us denote $\langle u'^{2}\rangle $ as the variance of the powder avalanche velocity in the slope parallel direction
$\langle u'^{2}\rangle = \dfrac{1}{h}\int_0^hu'^{2}dz $
This can be considered as the total turbulent energy in the powder cloud. We now decompose the energy into two scales
$\langle u'^{2}\rangle =\langle u'^{2}\rangle _s + \langle u^{'2}\rangle _L$
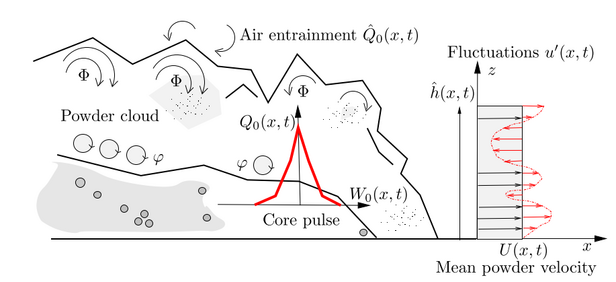
This decomposition allows to distinguish the turbulent kinetic energy in the layer near the avalanche core, and, the turbulent kinetic energy in the eddies near the cloud’s free surface (see Fig). We define two types of enstrophies (squared vorticity): ${\Phi } = \dfrac{\langle u^{'2}\rangle _L}{h^2}$ is the enstrophy of large eddies formed near the free surface and $\varphi = \dfrac{\langle u^{'2}\rangle _s}{h^2}$ is the enstrophy of eddies caused by shearing of the granular core. The enstrophy arising from the interaction with the core $\varphi(t) $ is time-dependent because it depends on the production and decay of random energy in the avalanche core. Some of this energy is transferred to the powder cloud. For example, the model predicts that significant turbulence is generated as the core descends steep slopes in the transition zones where the production of random energy from granular shearing is large. In this case enstrophy is transferred with the mass (air-dust mixture) that is exchanged between the core and cloud. We additionally take
$C_{e}=C_f+\frac{C_{r}\Phi}{\varphi +\Phi }$
The coefficient $C_{r}$ is the dissipation coefficient in the large scale eddies near the cloud’s free surface; $C_f$ is the coefficient governing frictional resistance in the cloud. The total specific energy $E$ without taking in account the air entrainment, internal energy $e$, and the total "pressure" $p$ (we call it "pressure" by analogy with the Euler equations of compressible fluids even if the dimension of $p$ is not the same as that of a pressure) are defined as
$E = \frac{1}{2}U^2 + e, \; e = \frac{1}{2}\left(gh + (\varphi + \Phi)h^2\right).$
$p = \frac{gh^2}{2} + (\varphi + \Phi)h^3.$
The second term in the expression of internal energy $e$ is the sum of the "turbulent" kinetic energy in the free surface $\frac{1}{2}\Phi h^2 $, and "turbulent" kinetic energy in the core/cloud boundary layer $\frac{1}{2}\varphi h^2 $.
To find the free-surface turbulence it is necessary to solve an additional differential equation for the depth-averaged energy $E$
$\frac{\partial \left( hE \right) }{{\partial t}} + \frac{\partial \left( hU E + pU \right) }{{\partial x}} = -C_e|U|^3 + Q_0W_0U+Q_0 \left( gh - \dfrac{U^2}{2} + \dfrac{3}{2} (\varphi +\Phi) h^2 \right) $
Here $h=h(x,t)$ is the avalanche height; $U(x,t)$ the powder cloud velocity, $t$ is the time, $C_f$ is the friction coefficient corresponding to the dissipation in the momentum equation. The source term $Q_0(x,t)$ for mass influx and velocity $W_0$ are given by the dynamics of the avalanche core. For more details, please see Ivanova and others (2022).
The introduction of turbulence improves the applicability of depth-averaged approaches. Long-wave approximation powder avalanche models suffer from the fact that they only predict a single slope-velocity is used to describe the propagation speed of the cloud. In addition, analytical velocity and density profiles are required to model the three-dimensional properties of the cloud. By predicting the state of spatial and temporal properties of the turbulence, it might be possible to better define more accurate $z$-direction velocity distributions. Presently, ad-hoc air-entrainment models are applied to model the height growth (and therefore density distribution) within the cloud. In future, it should be possible to link air-entrainment to the free-surface turbulence parameter. Thus, better predictions of avalanche impact pressure are possible.
Publications ¶
Ivanova, K., Caviezel, A., Bühler, Y., & Bartelt, P. (2022). Numerical modelling of turbulent geophysical flows using a hyperbolic shear shallow water model: application to powder snow avalanches. Computers and Fluids, 233, 105211 (9 pp.). https://doi.org/10.1016/j.compfluid.2021.
Bartelt, P., Buser, O., Vera Valero, C., & Bühler, Y. (2016). Configurational energy and the formation of mixed flowing/powder snow and ice avalanches. Annals of Glaciology, 57(71), 179-188. doi.org/10.3189/2016AoG71A464
Bartelt, P., Christen, M., Bühler, Y., Caviezel, A., & Buser, O. (2018). Snow entrainment: avalanche interaction with an erodible substrate. In International snow science workshop proceedings 2018 (pp. 716-720).
Bartelt, P., Bebi, P., Feistl, T., Buser, O., & Caviezel, A. (2018). Dynamic magnification factors for tree blow-down by powder snow avalanche air blasts. Natural Hazards and Earth System Science, 18(3), 759-764. https://doi.org/10.5194/nhess-18-759-2018
Caviezel, A., Margreth, S., Ivanova, K., Sovilla, B., & Bartelt, P. (2021). Powder snow impact of tall vibrating structures. In M. Papadrakakis & M. Fragiadakis (Eds.), Compdyn 2021 proceedings (p. 19112 (13 pp.). Institute of Research & Development for Computational Methods in Engineering Sciences.