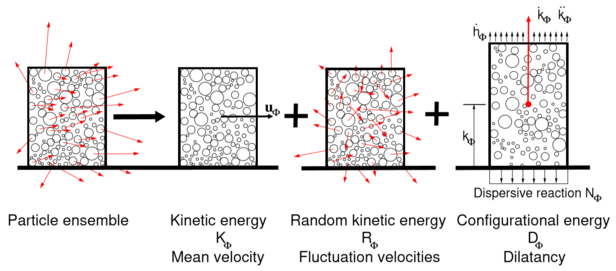
The RAMMS::EXT model applies the “random kinetic energy” (RKE) theory developed by Buser and Bartelt (2006, 2009, 2011, 2015) to model the avalanche core. The model splits the shear work rate into the production of thermal and granular temperatures. The granular temperature is the kinetic energy associated with the velocity fluctuations of the snow particles. When the random, non-directional particle motions encounter a hard basal boundary, they are redirected upwards, causing a change in the location of the center-of-mass of the flowing granular ensemble.
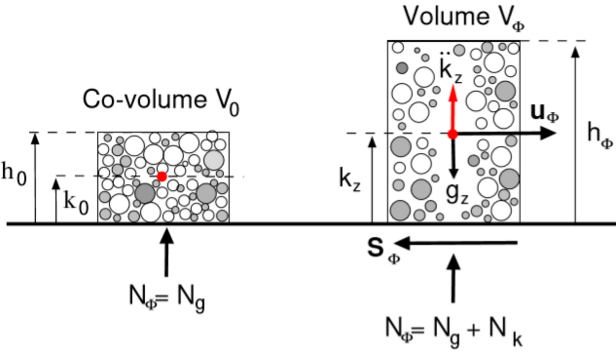
Moreover, the production of random kinetic energy (granular temperature) is accompanied by a change in the positions of the particles, and therefore a change in the potential and slope-perpendicular (z-direction) kinetic energy of the flowing particle ensemble. The sum of the kinetic energy (associated with the slope perpendicular velocity) and the potential energy we term the “configurational” energy of the avalanche core (Bartelt, 2016). Basically, a part of the shear work rate, changes the macroscopic locations and speed of the granules causing a dispersion, or expansion of the avalanche core, see Fig. 1 and Fig. 2 (the other part is used to change the microscopic properties, i.e. temperature of the granules). The macroscopic dispersion of snow particles is not slow, rather it is accompanied by explosive-type slope-perpendicular accelerations, leading to non-hydrostatic pressures and sudden changes in the core height (Fig. 2).
The slope perpendicular accelerations, which can be both expansive; that is, upward, or contractive; that is, downward, are responsible for the formation of disperse, “saltation” type flow configurations. Certain snow types, typically moist and wet snow, are so strongly damped, that the slope perpendicular accelerations are small, and therefore the avalanche core remains in a dense (contracted), plug-like flow configuration. This configuration is represented by the “co-volume” – the densest possible packing of granules (Fig. 2). With the RAMMS::EXT model it is therefore possible to model dense (frictional) or dispersive type flow regimes. Which regime is induced is dependent on the snow properties, primarily temperature and wetness, and terrain properties, slope steepness and roughness.