It has long been recognized that warm, moist snow behaves differently than cold, dry snow – leading to what Voellmy termed two “extreme” cases: dry, flowing/powder type avalanches and wet snow avalanches. Although the RAMMS::EXT model was primarily designed to model dry avalanches, it is also possible to model flowing wet avalanches (but not wet flow fingers!). In fact the mean temperature of the avalanche is always calculated.
To calculate the avalanche temperature, it is first necessary to specify the mean temperature of the release slab. This temperature is not the air temperature; it is also not the surface temperature of the snow slab. It is the temperature of the snow slab averaged over the height of the slab, which is often considerably warmer than the air or surface temperature.
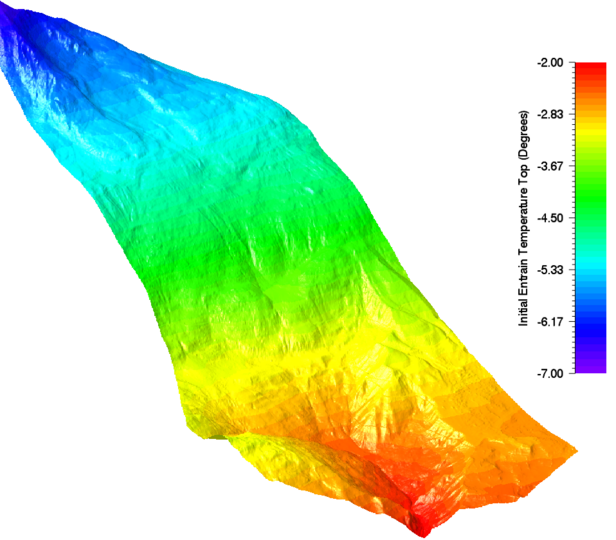
Because the avalanche entrains snow during its downward motion, the average temperature of the snowcover in the transition and runout zones must also be known. In the RAMMS::EXT model the temperature at a reference altitude is defined as well as the gradient of the temperature per 100m elevation drop. Typical reference temperatures for the Swiss Alps are provided in Table 1. Of course, these values will change in different climatic regions. Gradients in temperature are usually between DT= 0.3° C/100m and DT=0.5° C/100m. An example of an initial temperature distribution is shown in Figure 1.
Table 1: Recommended temperatures for Swiss Alps. When using the RAMMS::EXT model it is necessary to specify the snow temperature. For applications in Switzerland, we apply initial temperature values that are dependent on the elevation of the release zone.
| Elevation m.a.s.l | Recommended Snow Temperature (°C) |
| > 2'600 m | -7° |
| 2'500 m | -6° |
| 2'400 | -5°/-6° |
| 2'200 - 2'300 m | -5° |
| 1'900 - 2'100 m | -4° |
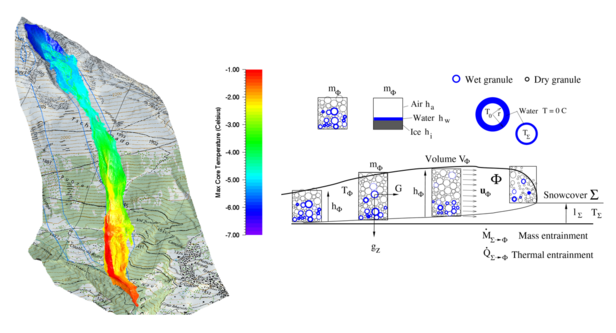
Temperature is a scale of the avalanche’s internal energy. RAMMS::EXT solves the internal energy balance equation, which takes into account the internal energy increase via friction (dissipation), decay of random energy (dissipation of random kinetic energy) and the entrainment of snow. As the entrainment algorithm assumes an ideal mixing, the heat energy of the entrained snow is included in the entrainment algorithm. Entrainment of warm, moist snow at lower elevations will thus increase the overall temperature of the avalanche, leading to an onset of melting. Solution of the internal energy equation assumes the existence of a “mean” temperature.
Although the mean temperature of the avalanche will vary from front to tail, there are also strong variations of temperature in the granular ensemble. Shearing interactions between granules is concentrated on the granule surface (Fig. 2). The heat produced during plastic deformation of the granule surface will not be immediately transported to the interior of the granule. This implies melting on the granule surface will begin before the mean temperature of the particle ensemble reaches T=0° C. In the RAMMS::EXT model melting begins when at a lower temperature (typically T=-2° C). Friction is proportional to the amount of meltwater bonded to the snow particles. The more the meltwater, the lower the Coulomb friction. The reduction of friction based on the amount of meltwater (lubrication) goes back to the original ideas of Voellmy.